
Determining causality is never perfect in the real world. but with well-designed empirical research, we can establish causation!ĭistinguishing between what does or does not provide causal evidence is a key piece of data literacy.
CORRELATION AND CAUSALITY SKIN
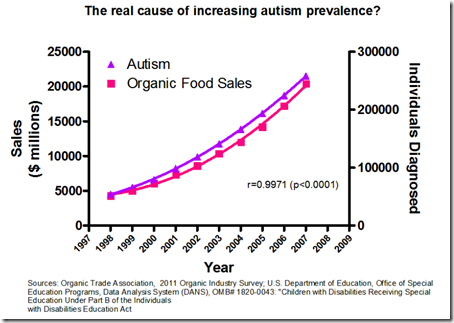
Both of the variables-rates of exercise and skin cancer-were affected by a third, causal variable-exposure to sunlight-but they were not causally related. At the same time, increased daily sunlight exposure means that there are more cases of skin cancer. This shows up in their data as increased exercise. Without exploring further, you might conclude that exercise somehow causes cancer! Based on these findings, you might even develop a plausible hypothesis: perhaps the stress from exercise causes the body to lose some ability to protect against sun damage.īut imagine that in reality, this correlation exists in your dataset because people who live in places that get a lot of sunlight year-round are significantly more active in their daily lives than people who live in places that don’t. This correlation seems strong and reliable, and shows up across multiple populations of patients. You observe a statistically significant positive correlation between exercise and cases of skin cancer-that is, the people who exercise more tend to be the people who get skin cancer. Imagine that you’re looking at health data. In fact, such correlations are common! Often, this is because both variables are associated with a different causal variable, which tends to co-occur with the data that we’re measuring. It’s possible to find a statistically significant and reliable correlation for two variables that are actually not causally linked at all.

However, correlations alone don’t show us whether or not the data are moving together because one variable causes the other. An example of causality is to say that smoking causes cancer, while an example of correlation would be to say that smoking is related to alcoholism.For observational data, correlations can’t confirm causation.Ĭorrelations between variables show us that there is a pattern in the data: that the variables we have tend to move together.Correlations are easier to establish compared to causalities.In this case, the variables are said to be correlated. While a correlation is a comparison or description of two or more different variables, but together. Causality refers to the cause and effect of a phenomenon, in which one thing directly causes the change of another.
Key Differences between Correlation and Causation Correlation does not imply causality, but it does help to suggest one. The austerity can only be accepted when there are sufficient clear reasons, otherwise it is always a good idea to use the correlation in place of causality. Practically, establishing a correlation is easier than establishing a clear causal relationship. In this case, the relationship is causal because there is a direct relationship between the employee and the money earned by him (and how he earns it).Ĭausality is more accurate than correlation, since correlation is simply a description of entities that change at the same time. Someone who works late and earns more money than a person who doesn’t. These conditions are related to the time of precedence, relationship and knowledge or experience.Īn example of a causal relationship is as follows: Three conditions must be true to claim that such a thing is the cause of something specific. One tends to derive this inference from correlation data. It is transitive in nature, meaning that if A is the cause of B and B is the cause of C, then A is the cause of C. However, this does not imply that the demand is due to the increase of the price or that the price has as only possible cause the increase of the demand since the price could be increasing because the raw material is also more expensive or any other factor.Ĭausality helps determine the existence of a relationship between variables.

However, both demand and price are entities different but in this case they are varying together. The demand for a product rises, so its price also tends to rise. An example of positive correlation is as follows: On the other hand, in a negative correlation, frequencies exhibit inverse characteristics (one variable increases and another decreases). A positive correlation is one in which if the frequency of one variable increases, then the same change is reflected in the other.


 0 kommentar(er)
0 kommentar(er)
